Euclidean Distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space (or even any inner product space) becomes a metric space. The associated norm is called the Euclidean norm. Older literature refers to the metric as Pythagorean metric.

Despite the development of numerous types of geometry, Euclidean distance is still by far the most geometrical tool of applied scientists. For example, statisticians find it useful to calculate the proximity between samples.

Application in Co-ordinate Geometry:

In one-dimension: Euclidean distance will be the absolute value of their numerical difference.

Euclidean Distance = I x-y I

In two-dimension:

If u=(x1,y1) and v=(x2,y2) are two points on the plane, their Euclidean distance is given by

Euclidean Distance= sqrt [ (x1−x2)²+(y1−y2)² ]

Geometrically, it's the length of the segment joining u and v.

In three-dimension:

In three-dimensional Euclidean space, the distance is

Euclidean Distance= sqrt [ (x1−x2)²+(y1−y2)² + (z1-z2)² ]

In N dimensions:

In general, for an n-dimensional space, the distance is

Euclidean Distance= sqrt [ (a1−b1)²+(a2−b2)² + (a1-b2)² +….+ (an-bn)²]

Using the Euclidean distances, we can create what is known as the Euclidean Distance Matrix. A Euclidean distance matrix is a matrix (two-dimensional array) containing the Euclidean distances, taken pair-wise, between a set of points. This matrix will have a size of N×N where N is the number of objects.This matrix is symmetric in nature – that is Xi,j = Xj,I.

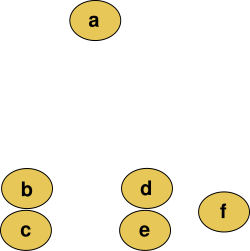
Example:

Below are various objects. Now we will calculate the Euclidean distance between each of them, pair wise

The Euclidean distance matrix would be:

	a	b	c	d	e	f
a	0	184	222	177	216	231
b	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
e	216	128	121	46	0	83
f	231	200	203	83	83	0

Posted by

Saurabh Agarwal

Finance